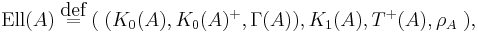Approximately finite dimensional C*-algebra
In C*-algebras, an approximately finite dimensional, or AF, C*-algebra is one that is the inductive limit of a sequence of finite dimensional C*-algebras. Approximate finite dimensionality was first defined and described combinatorially by Bratteli. Elliott gave a complete classification of AF algebras using the K0 functor whose range consists of certain type of abelian groups.
Contents |
Definition and basic properties
Finite dimensional C*-algebras
An arbitrary finite dimensional C*-algebra A takes the following form, up to isomorphism:
where Mi denotes the full matrix algebra of i × i matrices.
Up to unitary equivalence, a unital *-homomorphism Φ : Mi → Mj is necessarily of the form
where r·i = j. The number r is said to be the multiplicity of Φ. In general, a unital homomorphism between finite dimensional C*-algebras
is specified, up to unitary equivalence, by a t × s matrix of partial multiplicities (rl k) satisfying, for all l
In the non-unital case, the equality is replaced by ≤. Graphically, Φ, equivalently (rl k), can be represented by its Bratteli diagram. The Bratteli diagram is a directed graph with nodes corresponding to each nk and ml and the number of arrows from nk to ml is the partial multiplicity rlk.
Consider the category whose objects are isomorphism classes of finite dimensional C*-algebras and whose morphisms are *-homomorphisms modulo unitary equivalence. By the above discussion, the objects can be viewed as vectors with entries in N and morphisms are the partial multiplicity matrices.
AF algebras
A C*-algebra is AF if it is the direct limit of a sequence of finite dimensional C*-algebras:
where each Ai is a finite dimensional C*-algebra and the connecting maps αi are *-homomorphisms. We will assume that each αi is unital. The inductive system specifying an AF algebra is not unique. One can always drop to a subsequence. Suppressing the connecting maps, A can also be written as
The Bratteli diagram of A is formed by the Bratteli diagrams of {αi} in the obvious way. For instance, the Pascal triangle, with the nodes connected by appropriate downward arrows, is the Bratteli diagram of an AF algebra. A Bratteli diagram of the CAR algebra is give on the right. The two arrows between nodes means each connecting map is an embedding of multiplicity 2.
If an AF algebra A = (∪nAn)- , then an ideal J in A takes the form ∪n (J ∩ An)-. In particular, J is itself an AF algebra. Given a Bratteli diagram of A and some subset S of nodes, the subdiagram generated by S gives inductive system that specifies an ideal of A. In fact, every ideal arises in this way.
Due to the presence of matrix units in the inductive sequence, AF algebras have the following local characterization: a C*-algebra A is AF if and only if A is separable and any finite subset of A is "almost contained" in some finite dimensional C*-subalgebra.
The projections in ∪nAn in fact form an approximate unit of A.
The extension of an AF algebra by another AF algebra is again AF.
Classification
K0
The K-theoretic group K0 is an invariant of C*-algebras. It has its origins in topological K-theory and serves as the range of a kind of "dimension function." For an AF algebra A, K0(A) can be defined as follows. Let Mn(A) be the C*-algebra of n × n matrices whose entries are elements A. Mn(A) can be embedded into Mn + 1(A) canonically, into the "upper left corner". Consider the algebraic direct limit
Denote the projections (self-adjoint idempotents) in this algebra by P(A). Two elements p and q are said to be Murray-von Neumann equivalent, denoted by p ~ q, if p = vv* and q = v*v for some partial isometry v in M∞(A). It is clear that ~ is an equivalence relation. Define a binary operation + on the set of equivalences P(A)/~ by
where ⊕ is the orthogonal direct sum. This makes P(A)/~ a semigroup that has the cancellation property. We denote this semigroup by K0(A)+. Performing the Grothendieck group construction gives an abelian group, which is K0(A).
K0(A)+ carries a natural order structure: we say [p] ≤ [q] if p is Murray-von Neumann equivalent to a subprojection of q. This makes K0(A) an ordered group whose positive cone is K0(A)+.
For example, for a finite dimensional C*-algebra
one has
Two essential features of the mapping A ↦ K0(A) are:
- K0 is a (covariant) functor. A *-homomorphism α : A → B between AF algebras induces a group homomorphism α* : K0(A) → K0(B). In particular, when A and B are both finite dimensional, α* can be identified with the partial multiplicities matrix of α.
- K0 respects direct limits. If A = ∪nαn(An)-, then K0(A) is the direct limit ∪nαn*(K0(An)).
The dimension group
Since M∞(M∞(A)) is isomorphic to M∞(A), K0 can only distinguish AF algebras up to stable isomorphism. For example, M2 and M4 are not isomorphic but stably isomorphic; K0(M2) = K0(M4) = Z.
A finer invariant is needed to detect isomorphism classes. For an AF algebra A, we define the scale of K0(A), denoted by Γ(A), to be the subset whose elements are represented by projections in A:
When A is unital with unit 1A, the K0 element [1A] is the maximal element of Γ(A).
The triple (K0, K0+, Γ(A)) is called the dimension group of A. If A = Ms, its dimension group is (Z, Z+, [1, 2,... s]).
A group homomorphism between dimension group is said to be contractive if it is scale-preserving. Two dimension group are said to be isomorphic if there exists a contractive group isomorphism between them.
The dimension group retains the essential properties of K0:
- A *-homomorphism α : A → B between AF algebras in fact induces a contractive group homomorphism α* on the dimension groups. When A and B are both finite dimensional, corresponding to each partial multiplicities matrix ψ, there is a unique, up to unitary equivalence, *-homomorphism α : A → B such that α* = ψ.
- If A = ∪nαn(An)-, then the dimension group of A is the direct limit of those of An.
Elliott's theorem
Elliott's theorem says that the dimension group is a complete invariant of AF algebras: two AF algebras A and B are isomorphic if and only if their dimension groups are isomorphic.
Two preliminary facts are needed before one can sketch a proof of Elliott's theorem. The first one summarizes the above discussion on finite dimensional C*-algebras.
Lemma For two finite dimensional C*-algebras A and B, and a contractive homomorphism ψ: K0(A) → K0(B), there exists a *-homomorphism φ: A → B such that φ* = ψ, and φ is unique up to unitary equivalence.
The lemma can be extended to the case where B is AF. A map ψ on the level of K0 can be "moved back", on the level of algebras, to some finite stage in the inductive system.
Lemma Let A be finite dimensional and B AF, B = (∪nBn)-. Let βm be the canonical homomorphism of Bm into B. Then for any a contractive homomorphism ψ: K0(A) → K0(B), there exists a *-homomorphism φ: A → Bm such that βm* φ* = ψ, and φ is unique up to unitary equivalence in B.
The proof of the lemma is based on the simple observation that K0(A) is finitely generated and, since K0 respects direct limits, K0(B) = ∪n βn* K0 (Bn).
Theorem (Elliott) Two AF algebras A and B are isomorphic if and only if their dimension groups (K0(A), K0+(A), Γ(A)) and (K0(B), K0+(B), Γ(B)) are isomorphic.
The crux of the proof has become known as Elliott's intertwining argument. Given an isomorphism between dimension groups, one constructs a diagram of commuting triangles between the direct systems of A and B by applying the second lemma.
We sketch the proof for the non-trivial part of the theorem, corresponding to the sequence of commutative diagrams on the right.
Let Φ: (K0(A), K0+(A), Γ(A)) → (K0(B), K0+(B), Γ(B)) be a dimension group isomorphism.
- Consider the composition of maps α1* Φ : K0(A1) → (K0(B). By the previous lemma, there exists B1 and a *-homomorphism φ1: A1 → B1 such that the first diagram on the right commutes.
- Same argument applied to β1* Φ-1 shows that the second diagram commutes for some A2.
- Comparing diagrams 1 and 2 gives diagram 3.
- Using the property of the direct limit and moving A2 further down if necessary, we obtain diagram 4, a commutative triangle on the level of K0.
- For finite dimensional algebras, two *-homomorphisms induces the same map on K0 if and only if they are unitary equivalent. So, by composing ψ1 with a unitary conjugation if needed, we have a commutative triangle on the level of algebras.
- By induction, we have a diagram of commuting triangles as indicated in the last diagram. The map φ: A → B is the direct limit of the sequence {φn}. Let ψ: B → A is the direct limit of the sequence {ψn}. It is clear that φ and ψ are mutual inverses. Therefore A and B are isomorphic.
Furthermore, on the level of K0, the diagram on the left commutates for each k. By uniqueness of direct limit of maps, φ* = Φ.
The Effros-Handelman-Shen theorem
The dimension group of an AF algebra is a Riesz group. The Effros-Handelman-Shen theorem says the converse is true. Every Riesz group, with a given scale, arises as the dimension group of some AF algebra. This specifies the range of the classifying functor K0 for AF algebras and completes the classification.
Riesz groups
A group G with a partial order is called an ordered group. The set G+ of elements ≥ 0 is called the positive cone of G. One says that G is unperforated if k·g ∈ G+) implies g ∈ G+.
The following property is called the Riesz decomposition property: if x, yi ≥ 0 and x ≤ ∑ yi, then there exists xi ≥ 0 such that x = ∑ xi, and xi ≤ yi for each i.
A Riesz group (G, G+) is an ordered group that is unperforated and has the Riesz decomposition property.
It is clear that if A is finite dimensional, (K0, K0+) is a Riesz group, where Zk is given entrywise order. The two properties of Riesz groups are preserved by direct limits, assuming the order structure on the direct limit comes from those in the inductive system. So (K0, K0+) is a Riesz group for an AF algebra A.
A key step towards the Effros-Handelman-Shen theorem is the fact that every Riesz group is the direct limit of Zk 's, each with the canonical order structure. This hinges on the following technical lemma, sometimes referred to as the Shen criterion in the literature.
Lemma Let (G, G+) be a Riesz group, φ: (Zk, Zk+) → (G, G+) be a positive homomorphism. Then there exists maps σ and ψ, as indicated in the diagram to the right, such that ker(σ) = ker(φ).
Corollary Every Riesz group (G, G+) can be expressed as a direct limit
where all the connecting homomorphisms in the directed system on the right hand side are positive.
The theorem
Theorem If (G, G+) is a countable Riesz group with scale Γ(G), then there exists an AF algebra A such that (K0, K0+, Γ(A)) = (G, G+, Γ(G)). In particular, if Γ(G) = [0, uG] with maximal element uG, then A is unital with [1A] = [uG].
Consider first the special case where Γ(G) = [0, uG] with maximal element uG. Suppose
Dropping to a subsequence if necessary, let
where φ1(u1) = uG for some element u1. Now consider the order ideal G1 generated by u1. Because each H1 has the canonical order structure, G1 is a direct sum of Z 's (with the number of copies possible less than that in H1). So this gives a finite dimensional algebra A1 whose dimension group is (G1 G1+, [0, u1]). Next move u1 forward by defining u2 = φ12(u1). Again u2 determines a finite dimensional algebra A2. There is a corresponding homomorphism α12 such that α12* = φ12. Induction gives a directed system
whose K0 is
with scale
This proves the special case.
A similar argument applies in general. Observe that the scale is by definition a directed set. If Γ(G) = {vk}, one can choose uk ∈ Γ(G) such that uk ≥ v1 ... vk. The same argument as above proves the theorem.
Examples
By definition, uniformly hyperfinite algebras are AF and unital. Their dimension groups are the countable subgroups of R. For example, for the 2 × 2 matrices M2, K0(M2) is Z[½], the rational numbers of the form a/2. The scale is Γ(M2) = Z[½] ∩ [0, 1] = [0, ½, 1]. For the CAR algebra A, K0(A) is the dyadic rationals with scale K0(A) ∩ [0, 1], with 1 = [1A]. All such groups are simple, in a sense appropriate for ordered groups. Thus UHF algebras are simple C*-algebras. In general, the groups which are not dense are the dimension groups of Mk for some k.
Commutative C*-algebras, which were characterized by Gelfand, are AF precisely when the spectrum is extremely disconnected. The continuous functions C(X) on the Cantor set X is one such example.
Elliott's classification program
It was proposed by Elliott that other classes of C*-algebras may be classifiable by K-theoretic invariants. For a C*-algebra A, the Elliott invariant is defined to be
where T+(A) is the tracial positivel linear functionals in the weak-* topology, and ρA is the natural pairing between T+(A) and K0(A).
The original conjecture by Elliott stated that the Elliott invariant classifies simple unital separable nuclear C*-algebras.
In the literature one can find several conjectures of Elliott type, with corresponding modified/refined Elliott invariants.
Von Neumann algebras
In a related context, an approximately finite dimensional, or hyperfinite, von Neumann algebra is one with a separable predual and contains a weakly dense AF C*-algebra. Murray and von Neumann showed that, up to isomorphism, there exists a unique hyperfinite type II1 factor. Connes obtained the analogous result for the II∞ factor. Powers exhibited a family of non-isomorphic type III hyperfinite factors with cardinality of the continuum. Today we have a complete classification of hyperfinite factors.
References
- Bratteli, O. (1972), Inductive limits of finite dimensional C*-algebras, Trans. Amer. Math. Soc. 171, 195-234.
- Davidson, K.R. (1996), C*-algebras by Example, Field Institute Monographs 6, American Mathematical Society.
- Effros, E.G., Handelman, D.E. and Shen C.L. (1980), Dimension groups and their affine representations, Amer. J. Math. 102, 385-402.
- Elliott, G.A. (1976), On the classification of inductive limits of sequences of semi-simple finite dimensional algebras, J. Algebra 38, 29-44.
- Elliott, G.A. and Toms, A.S. (2008), Regularity properties in the classification program for separable amenable C-algebras, Bull. Amer. Math. Soc. 45, 229-245.
- Fillmore, P.A.(1996), A User's Guide for Operator Algebras, Wiley-Interscience.
- Rørdam, M. (2002), Classification of Nuclear C*-Algebras, Encyclopaedia of Mathematical Sciences 126, Springer-Verlag.
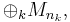
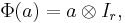
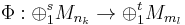
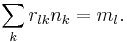
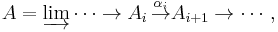
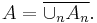
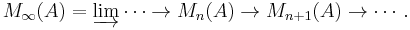
![[p] %2B [q] = [p \oplus q]](/2012-wikipedia_en_all_nopic_01_2012/I/5e7b5395bde9c85525f538fd11f83c63.png)
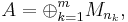
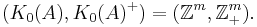
![\Gamma(A) = \{ [p] \,|\, p^* = p^2 = p \in A \} .](/2012-wikipedia_en_all_nopic_01_2012/I/93ef3f0bf96e137af6474b1bb26292f6.png)
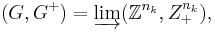
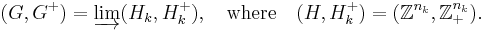
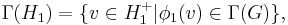
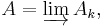
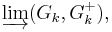
![\cup_k \phi_k [0, u_k] = [0, u_G].](/2012-wikipedia_en_all_nopic_01_2012/I/6f9d1cee7873621ab2ea49f70a437b5a.png)